Eine Funktion mit einer Gleichung, bei der die Variable x im Quadrat steht und der andere Term linear ist (bx), nennt man quadratische Funktion oder Funktion zweiten Grades.
Allgemeine Form
y = ax2 + bx + c (a ≠ 0) allgemeine Form der Gleichung einer quadratischen Funktion
a, b und c nennt man Koeffizienten der Funktion. Sie sind Elemente von R. a ≠ 0.
ax2 ist das quadratische Glied
bx ist das lineare Glied
c ist das konstante Glied
Die einfachste quadratische Funktion
Bei der einfachsten quadratischen Funktion ist a = 1, b = 0 und c = 0. Den Graphen nennen wir Normalparabel.


Die Parabel-Kurve geht durch den Nullpunkt (Ursprung). Ihre Arme sind symmetrisch und nach oben offen.
Sonderfälle der allgemeinen Form:
| (1) a = 1, b = 0 und c = 0 | y = x² | Normalparabel |
| (2) c ≠ 0 und b = 0 | y = x² + c | Verschiebung der Normalparabel entlang der y – Achse um c |
| (3) a > 0, c = 0 und b= 0 | y = ax² | die um a gestreckte oder gestauchte Normalparabel |
| (4) a = 1, d ≠ 0 und e ≠ 0 | y = (x + d)² + e | Verschiebung der Normalparabel entlang der y – Achse um e und entlang der x- Achse um d |
| (5) a = 1, b = p und c = q | y = x² + px + q | Normalform einer quadratischen Funktion |
| (6) a < 0, b ≠ 0 und c ≠ 0 | Parabel öffnet sich nach unten |
Die quadratische Funktion y = x²
Sonderfall der allgemeinen Form einer quadratischen Funktion für a = 1 und b = 0 und c = 0

Wichtige Eigenschaften der Funktion y = x²
| (1) | Definitionsbereich: x∈R |
| (2) | Wertebereich: y ∈ R und y≥0 |
| (3) | f (0) = 0 ist der kleinste Funktionswert. |
| (4) | Im Intervall x  > 0 fällt das Bild der Funktion monoton. > 0 fällt das Bild der Funktion monoton.Im Intervall x  >0 steigt das Bild der Funktion monoton. >0 steigt das Bild der Funktion monoton. |
| (5) | Das Bild der Funktion ist eine quadratische Parabel. → Normalparabel Das Bild liegt axialsymmetrisch zur y – Achse. |
Die quadratische Funktion y = ax² + c
Wie erhält man das Bild der Funktion y = ax² + c aus dem Bild der Funktion y = x² (Normalparabel)?
(1) Die Normalparabel wurde um „c“ Einheiten entlang der y – Achse verschoben.
(2) Die Normalparabel wurde um den Faktor „a“ gestreckt beziehungsweise gestaucht.
(3) Das Bild der Funktion y = ax² + c ist eine quadratische Parabel.
(4) Die Scheitelpunktkoordinaten sind: S (0 ; c)
(5) Wenn a < 0, dann öffnet die Parabel nach unten.
Fallunterscheidung
| (1) | a = 1 | → | Normalparabel y = x2 |
| (2) | a > 1 | → | Parabel gestreckt im Vergleich zur Normalparabel y = x2 |
| (3) | 1 > a > 0 | → | Parabel gestaucht im Vergleich zur Normalparabel y = x2 |
| (4) | a < 0 | → | Parabel an der x-Achse gespiegelt (öffnet nach unten) |

Beispiele
(1) y = 2x2 – 3

(2) y = 3,5x2 + 1,5

(3) y = – 4x2 + 2,5

(4) y = 0,4x2 – 3,5

Die quadratische Funktion y = (x+d)2 + c
Grafische Darstellung der Funktion mit Hilfe der Normalparabel (Schablone). Notwendig sind: Scheitelpunktkoordinaten S (x;y) → S (-d;e)
Ziel
Ermittle aus der Normalform einer quadratischen Gleichung y = f (x) die Form y = (x + d)² + e, lese daraus die Scheitelpunktkoordinaten S (-d;e) ab und stelle die Funktion mit Hilfe der Schablone der Normalparabel grafisch dar!
Bilde dazu die quadratische Ergänzung!
Beispiel
y = x2 – 6x + 7
 quadratische Ergänzung zu (x² – 6x) bestimmen quadratische Ergänzung zu (x² – 6x) bestimmen |  | Eine „quadratische Ergänzung“ macht einen Term der Form x² + p zu einem vollständigen Quadrat der Form (x + p)² |
| y = x² – 6x + (3² – 3²) + 7 |  | Man ermittelt die “ quadratische Ergänzung „, indem man das Quadrat von p/2 bildet! Damit man die „quadratische Ergänzung“ dem Term bedenkenlos hinzufügen kann, muss man sie |
 umformen umformen | gleichzeitig wieder subtrahieren! Hier: (3² – 3²) | |
y = (x² – 6x + 3²) – 9 + 7 vollständiges Quadrat angeben y = (x – 3)2 – 2 vollständiges Quadrat angeben y = (x – 3)2 – 2  Scheitelpunktkoordinaten S (– d; e) angeben Scheitelpunktkoordinaten S (– d; e) angebeny = (x – 3)2 – 2 y = (x + d)2 + e d = – 3 – d = 3 und e = – 2 |
→ S (3;-2) Scheitelpunktkoordinaten

Hier ein weiteres Beispiel
y = x2 + 4x + 3
y = x² + 4x + (2² – 2²) + 3
y = (x² + 4x +2²) – 4 + 3
y = (x + 2)² – 1
S (-2;-1)

Die Normalform einer quadratischen Funktion:
y = x2 + px + q
Ziel
Überführe die Normalform einer quadratischen Funktion in eine Funktion mit der Gleichung
y = (x + d)² + e!
y = (x + p/2)² – (p/2)² +q → y = (x + p/2)² – p²/4 + q → y = (x + p/2)² – (p²/4 – q)
Beschreibung: d = p/2 und q = p²/4 – q
Scheitelpunktkoordinaten: S (– p/2; q – p²/4)
Merke
Die Differenz p²/4 – q nennt man die Diskriminante D der betreffenden quadratischen Funktion. Jede quadratische Funktion y = x² + px + q hat als Graph eine zur Normalparabel kongruente Parabel mit dem Scheitelpunkt S (-p/2; q – p²/4) bzw. S (-p/2; – D).
Jede Funktion y = x² + px + q nimmt also an der Stelle xS = –p/2 ihren kleinsten
Funktionswert yS = -D an.
Für x  –p/2 ist die Funktion monoton fallend und für x
–p/2 ist die Funktion monoton fallend und für x  –p/2 monoton wachsend.
–p/2 monoton wachsend.
Nullstellen der quadratischen Funktion
y = x2 + px + q
Merke:
Jede quadratische Funktion y = x² + px + q hat genau dann Nullstellen, wenn für die Diskriminante D gilt: D = p²/4 – q ≥ 0 .
Fallunterscheidung:
| D = p²/4 – q | ys = – D | Parabel y = x² + px + q | Funktion y = x2 + px + q |
| D > 0 | ys < 0 | schneidet die x-Achse in zwei verschiedenen Punkten | hat genau zwei verschiedene Nullstellen |
| D = 0 | ys = 0 | berührt die x-Achse | hat genau eine Nullstelle |
| D < 0 | ys > 0 | hat keine gemeinsamen Punkte mit der x-Achse | hat keine Nullstellen |
Beispielaufgabe:
Diskutiere ohne eine grafische Darstellung die quadratische Funktion y = x2 + 4x + 1 hinsichtlich:
a) Scheitelpunktkoordinaten
b) Wertebereich
c) Definitionsbereich
d) Monotonieverhalten
e) Existenz von Nullstellen
f) kleinster Funktionswert (Minimum)
Lösung
y = x2 + 4x + 1 → y = (x + 2)2 – 3
a) S(-2; -3)
b) y  –3
–3
c) –  x
x 
d) monoton fallend: x  -2 und monoton steigend: x
-2 und monoton steigend: x  –2
–2
e) D = 3 → 2 Nullstellen
f) ymin = –3
Berechnung der Nullstellen der
quadratischen Funktion y = x² + px + q
allgemein
y = x² + px + q → y = 0 → 0 = x² + px + q (quadratische Gleichung in der Normalform)
Anwendung der allgemeinen Lösungsformel: x1/2 = –p/2 ± √(p/2)² – q
Lösungen der quadratischen Gleichung: x1 = –p/2 + √(p/2)² – q
x2 = –p/2 – √(p/2)² – q
Nullstellen der zugehörigen quadratischen Funktion: x01 = –p/2 +√(p/2)2 – q
x02 = – p/2 – √(p/2)2 – q
am Beispiel
Gib die Nullstellen der quadratischen Funktion y = x2 + 6x + 5 durch Lösung der zugehörigen quadratischen Gleichung an!
y = x2 + 6x + 5 → y = 0 → 0 = x2 + 6x + 5
Anwendung der allgemeinen Lösungsformel: x1/2 = – p/2 ± √(p/2)2 – q
x1/2 = – 6/2 ± √(6/2)2 – 5
Lösungen der quadratischen Gleichung:
x1 = –3 – 2 = –5
x2 = –3 + 2 = –1
Nullstellen der zugehörigen quadratischen Funktion:
x01 = – 5
X02 = – 1
Zur Kontrolle die graphische Darstellung der Funktion:
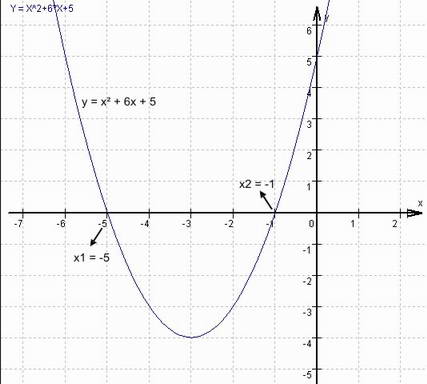
Merke:
Die Nullstellen der quadratischen Funktion y = x² + px + q entsprechen den Lösungen der zugehörigen quadratischen Gleichung x² + px + q = 0.
Ermittlung der Funktionsgleichung y = x² + px + q
bei zwei gegebenen Punkten P und Q
Aufgabe
Ermittle die Gleichung einer quadratischen Funktion in der Normalform y = x² + px + q, wenn vom Funktionsbild zwei Punkte P und Q bekannt sind, die diese Funktion erfüllen: P(5;6) und Q(2;3)! Forme die ermittelte Normalform in die Form y = (x + d)² + e um und stelle die Funktion grafisch dar!
Lösung
Punktkoordinaten von P und Q jeweils in die Funktionsgleichung (y = x² + px + q) einsetzen
→ es ergibt sich ein lineares Gleichungssystem (2 Gleichungen mit 2 Unbekannten)
I. 6 = 5² + 5p + q
II. 3 = 2² + 2p + q
→ beide Gleichungen (z. B.) nach „q“ umformen und dann gleichsetzen
I. q = -19 -5p
II. q = -1 – 2p
I = II: – 19 -5p = -1 – 2p → Gleichung nach p umformen → p = -6
p in Gleichung I oder II einsetzen und nach q umformen → q = 11
Funktionsgleichung: y = x² – 6x + 11
Scheitelpunktkoordinaten S(-d;e) aus y = (x + d)² + e ermitteln
y = x² – 6x + 11 → y = x² – 6x + 11 + 3² – 3³ → y = x2 – 6x + 32 + 11 – 32
y = (x – 3)2 + 2 → S(3;2)

Übungen
1. Ermittle die Gleichung einer quadratischen Funktion in der Normalform y = x2 + px + q, wenn vom Funktionsbild zwei Punkte A und B bekannt sind, die diese Funktion erfüllen: A(2;1) und B(5;4)! Forme die ermittelte Normalform in die Form y = (x + d)2 + e um und stelle die Funktion grafisch dar!
2. Diskutiere eine quadratische Funktion der Form y = x2 + px + q, von deren Graph lediglich zwei Punkte P(1;0) sowie Q(4;-3) bekannt sind, hinsichtlich:
a) Scheitelpunktkoordinaten
b) Wertebereich
c) Definitionsbereich
d) Monotonieverhalten
e) Existenz (Angabe) von Nullstellen
f) kleinster Funktionswert (Minimum)
g) Schnittpunkt mit der y-Achse
Zeichne zur Kontrolle das Bild der gesuchten quadratischen Funktion!
Zur Berechnung des Scheitelpunktes gibt es mehrere Wege, je nach Klassenstufe gibt es verschiedene Verfahren:
1. Das schnellste Verfahren ist das Ablesen aus der Scheitelpunktsform
Bsp.: f(x)=(x – 3)2 + 4
Die x – 3 gibt an, dass der Scheitelpunkt um 3 Einheiten nach rechts verschoben ist —> x-Koordinate (Wäre der Ausdruck z.B. ‘x + 5’, dann wäre der Scheitelpunkt entsprechend 5 Einheiten nach links verschoben).
Die ^2 gibt an, dass es eine Parabel ist.
Die +4 gibt an, dass der Scheitelpunkt um 4 Einheiten nach oben verschoben ist —> y-Koordinate (Wäre der Ausdruck z.B. ‘-6’, dann wäre der Scheitelpunkt entsprechend 6 Einheiten nach unten verschoben).
=> Scheitelpunkt S(3/4)
2. Ist nur eine allgemeine Form der Parabel gegeben, kann mann diese in die Scheitelpunkts-Form zurückführen. Als Ansatz wäre hier Polynomdivision oder quadratische Ergänzung zu nennen. Ist aber ein eigenes Themenfeld von daher hier nicht weiter erläutert.
3. Die Differenzialrechnung führt immer, egal in welcher Form relativ schnell zur Lösung. Gegeben sei unsere obige Funktion in der allgemeinen Form:
Bsp.: f(x)=x2-6x+13
Durch Ableiten erhält man:
f'(x)=2x – 6
Setzt man diese (erste) Ableitung Null, so erhält man:
f’(x)=0
0=2x-6
6=2x
x=3 → x-Koordinate
Durch einsetzen der x-Koordinate in unsere Ausgangsfunktion erhält man:
f(3)=3²-63+13
f(3)=4 —> y-Koordinate
⇒ Scheitelpunkt S(3/4)
Lösungen:
zu 1.
P(2;1) und Q(5;4)
I. 1 = 2² + 2p + q
II. 4 = 5² + 5p + q
I. q = 1 – 4 – 2p q = -3 – 2p
II. q = 4 – 25 -5p q = -21 – 5p
I = II: -3 – 2p = -21 – 5p ? p = -6 ? q = 9
→ y = x² – 6x + 9
→ S(-d;e) y = x² -6x + 9 + 3² – 3² ? y = (x – 3)²
→ S(3;0)
zu 2.
P(1;0) und Q(4;-3)
I. 0 = 1² + 1p + q
II. -3 = 4² + 4p + q
I. q = 0 – 1² – 1p q = -1 – 1p
II. q = -3 – 4² – 4p q = -19 – 4p
I = II:
-1 – p = -19 – 4p ? p = -6 ? q = 5
y = x² – 6x + 5
S(-d;e) y = x2 -6x + 5 + 32 – 32 → y = (x – 3)² – 4
S(3;-4)
0 = x2 – 6x + 5 → x1/2 = 3 ± √(9 – 5)
x1 = 3 + 2 = 5
x2 = 3 – 2 = 1
a) S(3;–4)
b) –4 y 8
c) –8 x 8
d)
–∞ ≤ x ≤ 3 monoton fallend
3 ≤ x ≤ ∞ monoton steigend
e) x1 = 5 und x2 = 1
f) y min = – 4
g) Py(0;5)
zur Kontrolle:

Hier geht’s zurück zur Mathe-Seite